1. 短軸承理論

當(dāng)軸承寬度l遠(yuǎn)小于直徑d時(shí)，即可近似地把這種滑動(dòng)軸承視為無限短軸承。于是無量綱Reynold方程簡化為：

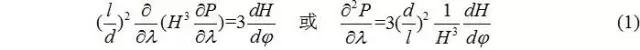
式中，φ—周向角度，0≤φ≤2π；λ—軸向無量綱寬度，-1≤λ≤1；H—無量綱油膜厚度。

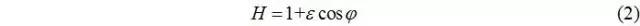
經(jīng)連續(xù)積分，并引入軸承兩側(cè)的邊界條件：λ=±1處，P=0，于是有：

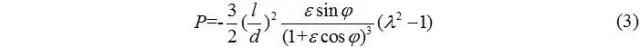
若引入Sommerfeld邊界條件，油膜整周均不破裂，則P為周期函數(shù)，終止邊界條件為：

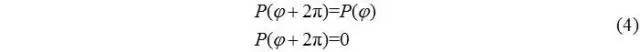
若引入半Sommerfeld條件，則終止邊界條件為：

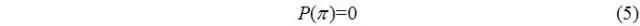
考慮到實(shí)際情況，采用半Sommerfeld條件求出性能數(shù)值，在0≤φ≤π上積分后得油膜合力兩分量的無量綱值：

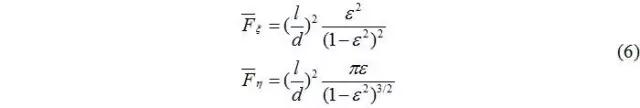
無量綱油膜壓力合力為：

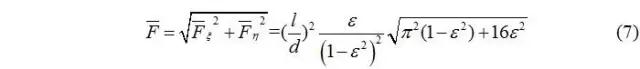
偏位角θ的解析式：

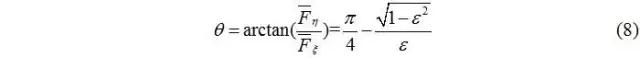
同時(shí)，短軸承理論可比無限寬軸承理論多算出一個(gè)性能數(shù)據(jù)，即側(cè)泄量：

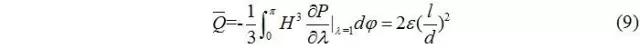
2. Matlab求解計(jì)算及分析

據(jù)式(3)-(5)，解得Sommerfeld條件以及半Sommerfeld條件的油膜壓力分布分別如圖1、圖2所示。

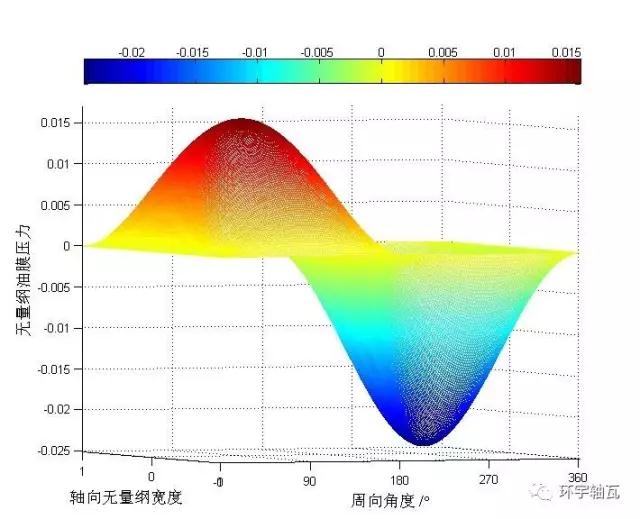
圖1 Sommerfeld條件油膜壓力分布

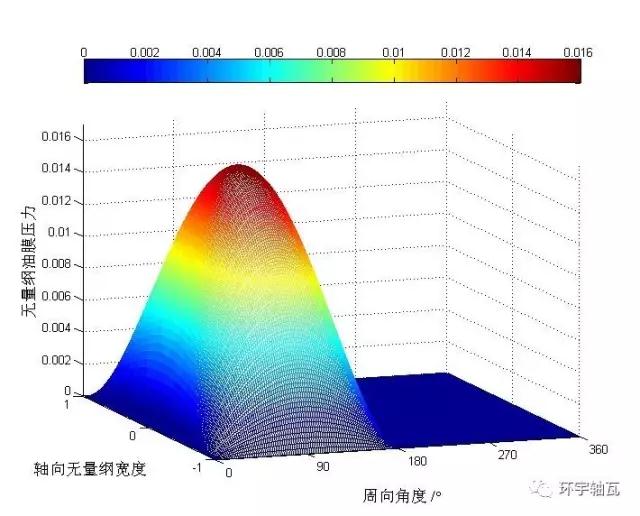
圖2 半Sommerfeld條件油膜壓力分布

Sommerfeld條件下π~2π區(qū)域出現(xiàn)負(fù)壓，表明此處油膜已破裂，且較之于Sommerfeld條件解，半Sommerfeld條件解恰為其解得0~π半周內(nèi)的正壓分布。

再據(jù)式(6)~(7)，以及式(8)，解得不同寬徑比(l/d)下油膜無量綱承載隨偏心率的變化曲線如圖3所示，同時(shí)得到偏位角隨偏心率的變化關(guān)系如圖4。

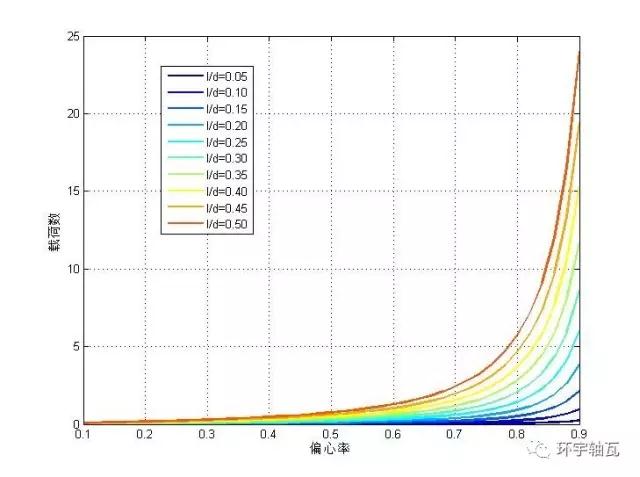
圖3 不同寬徑比載荷數(shù)隨偏心率的變化關(guān)系

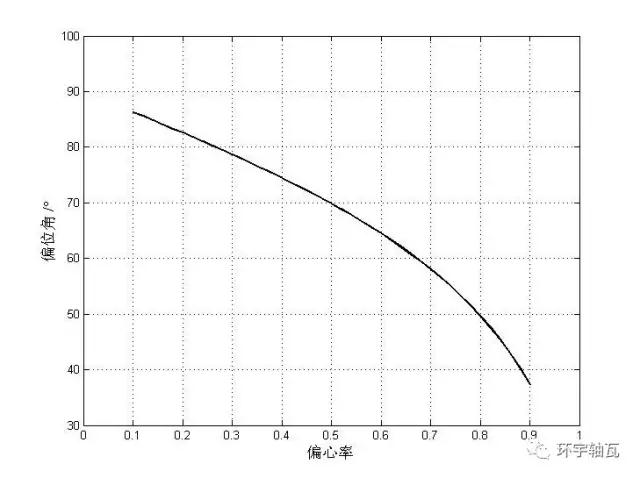
圖4 偏位角隨偏心率的變化關(guān)系

顯然，偏心率越大，油膜承載能力越強(qiáng)，且同一偏心率下，寬徑比越大，油膜承載能力越強(qiáng)：偏位角的數(shù)值只與偏心率有關(guān)；偏心率越大，偏位角越小。符合滑動(dòng)軸承經(jīng)典理論。

再據(jù)上，基于短軸承理論可計(jì)算出側(cè)泄量，側(cè)泄量、偏心率、寬徑比之間的變化關(guān)系如圖4。

由圖可知，無量綱測泄量與偏心率線性相關(guān)，且偏心率一定時(shí)，寬徑比越大，無量綱測泄量越大。

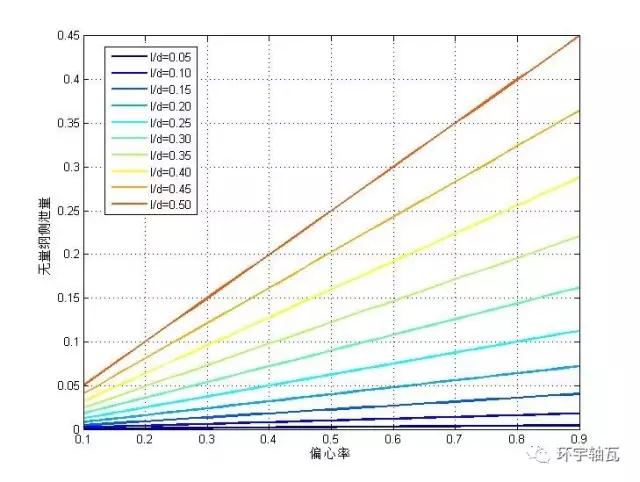
圖5 無量綱測泄量-偏心率的變化關(guān)系

3. 結(jié)語

短軸承理論在寬徑比(l/d)較小時(shí)有一定實(shí)用價(jià)值，l/d越小則其計(jì)算結(jié)果越準(zhǔn)，至今它仍用于滑動(dòng)軸承的分析和設(shè)計(jì)。