1. 引言

計算圓柱軸承特性時，一般先由Reynold方程解出壓力分布，然后積分求出承載力、阻力、流量等。為簡化求解數(shù)學模型，以定常工況下運轉(zhuǎn)，即：轉(zhuǎn)子載荷和轉(zhuǎn)速等均不隨時間而變，且具有等溫膜的油潤滑(μ=常數(shù)，ρ=常數(shù))的軸承等基本情況為例，應用無限寬軸承理論，可近似計算圓柱軸承油膜壓力分布以及靜特性。

2. 無限寬軸承理論

當軸承寬度l遠大于直徑d時，可近似認為油膜內(nèi)無軸向流動，壓力沿軸向均布，于是無量綱Reynold方程簡化為如下常微分方程(一維Reynold方程)：

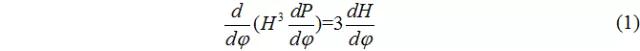
經(jīng)連續(xù)積分，并引入初始邊界條件：φ=0處，P=0，于是：

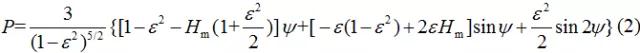
式中，Hm表示最大壓力Pmax處的油膜厚度，且Hm厚隨著采用終止邊界條件的不同而不同。

φ與ψ的變換關(guān)系為:

2.1 Sommerfeld條件

引入Sommerfeld邊界條件，設油膜整周均布破裂，則P為周期函數(shù)：

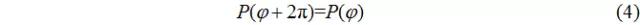
顯然，式(2)中非周期函數(shù)ψ的系數(shù)為0，即：

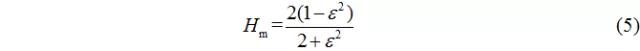
則可得Sommerfeld邊界條件圓柱軸瓦油膜壓力：

取微面積：

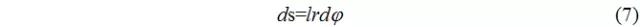
將微面積上力沿偏心方向及垂直方向兩個分量依次積分，即得油膜壓力的合力的兩個分量如圖1所示。

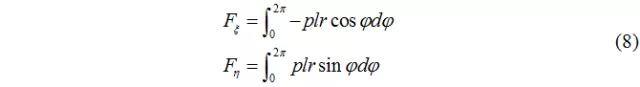
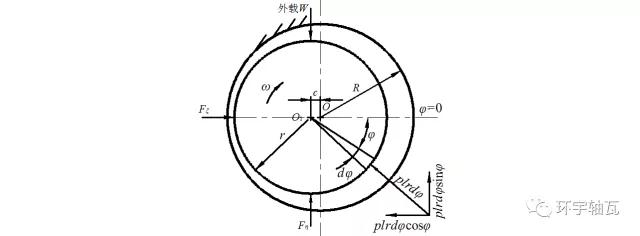
圖1 油膜力及其分量

積分后得油膜合力兩分量的無量綱值：

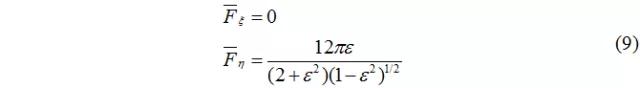
無量綱油膜壓力合力為：

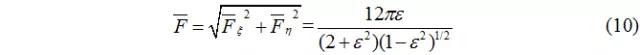
據(jù)式(9)施用Sommerfeld邊界條件的結(jié)果是油膜合力的方向總是垂直于偏心方向，雖然偏心率不同，但偏位角θ恒等于90°。

2.2 半Sommerfeld條件

若采用半Sommerfeld條件，則終止邊界條件為：

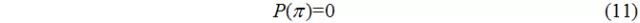
圓柱軸瓦油膜壓力：

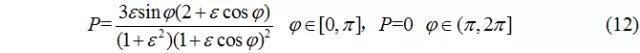
其壓力合成的無量綱力為：

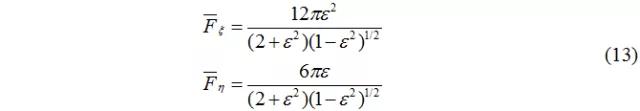
矢量合成無量綱油膜壓力合力：

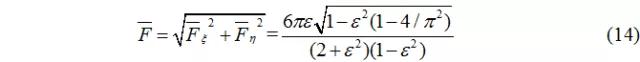
顯然，偏位角θ不再恒等于90°，其解析式：

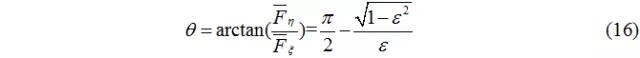
2. Matlab求解計算及分析

據(jù)式(6)和(12)利用Matlab數(shù)值計算軟件編程計算，解得Sommerfeld條件以及半Sommerfeld條件的油膜壓力分布分別如圖2、圖3所示。

由于Sommerfeld邊界條件不考慮油液軸向流動，因而其解與實際情況相差甚遠。較之于Sommerfeld條件解，半Sommerfeld條件解恰為其解得0~π半周內(nèi)的正壓分布。

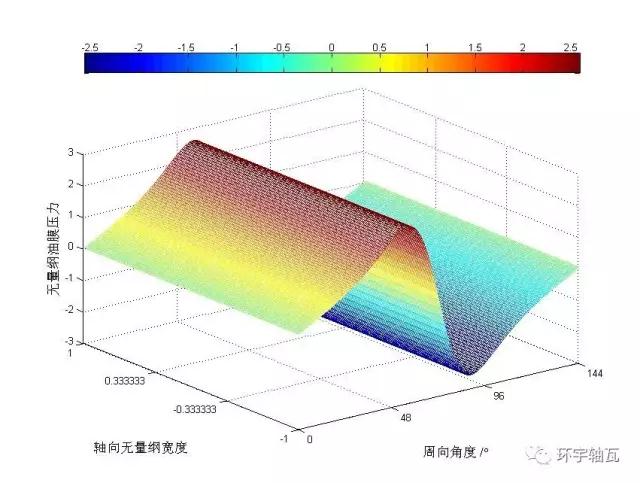
圖2  Sommerfeld條件油膜壓力分布圖

圖3  Sommerfeld條件油膜壓力分布圖

取不同偏心率，軸承油膜周向壓力分布如圖4、圖5所示。半Sommerfeld條件解依然為Sommerfeld條件解得0~π半周內(nèi)的正壓分布。

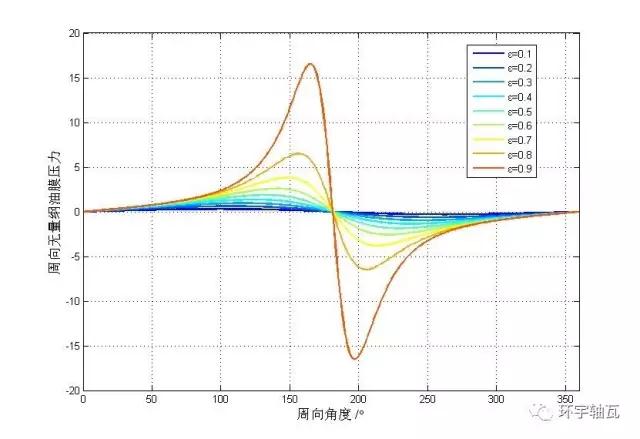
圖4  Sommerfeld條件周向油膜壓力

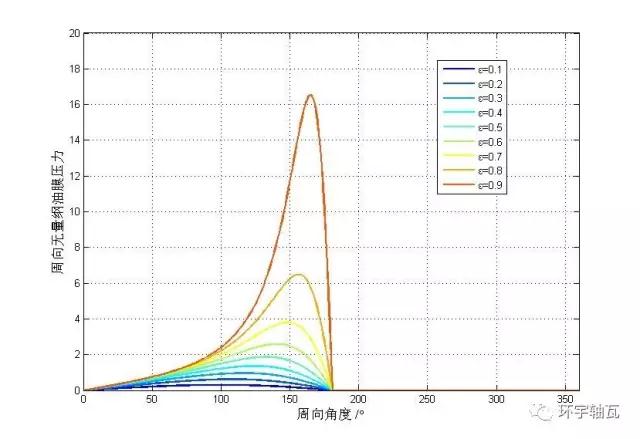
圖5  半Sommerfeld條件周向油膜壓力

再據(jù)式(8)~(11)，以及式(8)~(16)，解得兩種邊界條件下油膜無量綱承載隨偏心率的變化曲線，如圖6所示。

據(jù)此可知，偏心率越大，油膜承載峰值越大，承載能力越強，符合液體動壓軸承經(jīng)典理論。

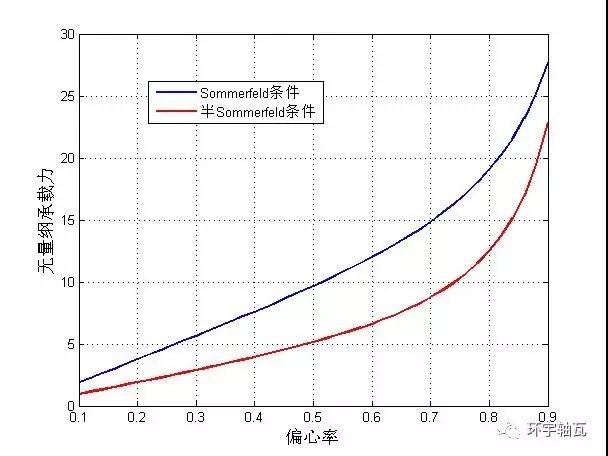
圖6 無量綱承載-偏心率變化關(guān)系

偏位角隨偏心率的變化關(guān)系如圖7所示。

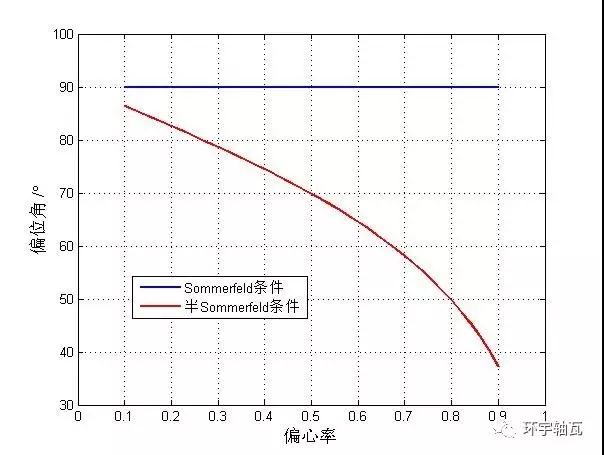
圖7 偏位角-偏心率變化關(guān)系

3. 結(jié)論

在過去的100多年里，研究者們對軸承潤滑性能進行了大量的探索研究，限于當時缺乏的先進的數(shù)值求解方法和計算技術(shù)，研究者們只能通過將軸承簡化為無限寬或無限窄的情況來求解軸承的潤滑性能，顯然這種解析解得到的結(jié)果與實際的軸承運行數(shù)據(jù)有較大的出入。雖與實際情況相差較遠，但其求解思路及方法對后來者學習、探索液體動壓軸承理論依然有著重要價值。